热点!什么是正四棱锥_正四棱锥的解释
 (资料图片仅供参考)
(资料图片仅供参考)
欢迎观看本篇文章,小柴来为大家解答以上问题。什么是正四棱锥,正四棱锥的解释很多人还不知道,现在让我们一起来看看吧!
1、四棱锥:底是正方形,边是四个全等的等腰三角形,有共同的顶点。顶点在底部的投影是底部的中心。底部是正方形,顶点在底部的投影就是正方形的中心。三角形的底边是正方形的边。
2、体积公式:hs 1/3 (h=高度,s=底面积)。
本文到此结束,希望对大家有所帮助。
关键词:
下一篇:最后一页
精心推荐
- 热点!什么是正四棱锥_正四棱锥的解释
- aptx4869配方是真的_aptx4869配方
- 今年,5件事关系养老、医保、工伤、失业等保险缴费以及待遇享受 天天最新
- 中国情侣在巴厘岛洲际酒店身亡,警方排除他人盗窃行凶可能|天天微头条
- 焦点讯息:2023年5月5日河南省聚羧酸系减水剂价格最新行情预测
- 亚冠决赛-浦和红钻1-0利雅得新月 总比分2-1夺队史第三座亚冠冠军 世界热点
- 每体:拉菲尼亚考虑夏窗离队,收到7-8千万欧报价巴萨才会放人_新动态
- 金融助力深圳新能源汽车产业跑出“加速度”|环球短讯
- 国内四大会计师事务所
- 全球报道:捂紧钱袋的年轻人,连零食都不吃了?
- 《银护3》北美创系列最佳提前场票房 内地则系列最差 焦点日报
- 四川:推广油菜新品种 助推油菜产业提质增效
- 万凯新材(301216.SZ):计划今年设立2个海外仓_环球微资讯
- 一架美国F-16战斗机在韩国坠毁
X 关闭
X 关闭
产业
-
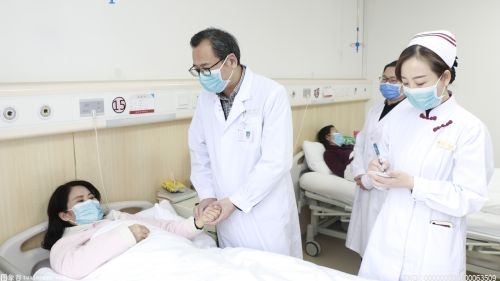
不用跑北京 在家门口也能挂上顶...
日前,我省首个神经疾病会诊中心——首都医科大学宣武医院河北医院...
-

“十四五”期间 河北省将优化快...
从省邮政管理局获悉,十四五期间,我省将优化快递空间布局,着力构...
-

张家口市宣化区:光伏发电站赋能...
3月19日拍摄的张家口市宣化区春光乡曹庄子村光伏发电站。张家口市宣...
-
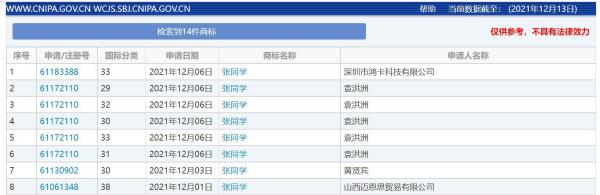
“张同学”商标被多方抢注 涉及...
“张同学”商标被多方抢注,官方曾点名批评恶意抢注“丁真” ...
-

山东济南“防诈奶奶团”花式反诈...
中新网济南12月15日电 (李明芮)“老有所为 无私奉献 志愿服...
-

广州新增1例境外输入关联无症状...
广州卫健委今日通报,2021年12月15日,在对入境转运专班工作人...
-

西安报告初筛阳性病例转为确诊病例
12月15日10:20,经陕西西安市级专家组会诊,西安市报告新冠病毒...
-
广东东莞新增本土确诊病例2例 ...
(抗击新冠肺炎)广东东莞新增本土确诊病例2例 全市全员核酸检测...
-

中缅边境临沧:民警深夜出击捣毁...
中新网临沧12月15日电 (胡波 邱珺珲)记者15日从云南临沧边境...
-

“土家鼓王”彭承金:致力传承土...
中新网恩施12月15日电 题:“土家鼓王”彭承金:致力传承土家...